2.4 The Precise Definition of a Limit

The intuitive definition of a limit gives us estimates that are as close to the exact answer as we might need. However, a more precise definition of the limit gives us the ability to get good estimates.

The precise definition of a limit says that if f is a function on an open interval that contains the number a, except possibly at a itself, then the limit of f(x) as x approaches a is L. We can write this as

Verbally, we can say that f(x) is close to L when x is close to a because we can make the values of f(x) within any distance from L by taking the values of x within a distance from a, but not equal to a. This is illustrated in the graph directly below.

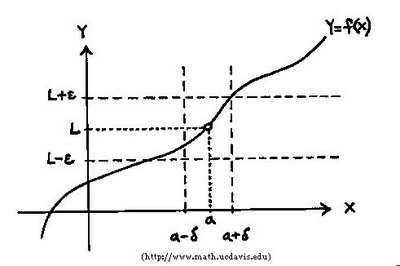
One sided limits can also be precisely defined.

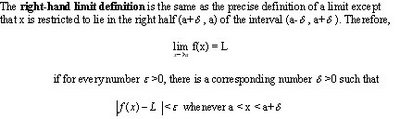
Infinite limits can also be precisely define by saying that if f is a function is on an open interval that contains the numbers around a, but excluding a, then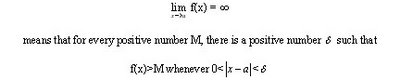
* Functions that become largely negative as x gets close to a have this definition: Let f be a function defined on an open interval that contains the number a, except possibly at a itself. Then

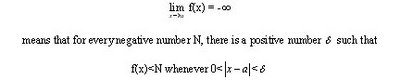
*For limits, one-sided limits, and infinite limits, we can use the precise definitions to prove the limits convincingly instead of vaguely as we do with intuitive definitions.

Additional Links:

Oregon State Limits

NCTU Limits

Reminder: Crystal, your turn next.