Section 2.5 Continuity

Section 2.5 Continuity

Well the title of this section tells all. As normal math section titles should.

Continuity's definition is lim x--> a f(x)=f(a). Basically, continuity is when you are able to follow a specified section of a graph without having any holes or jumps.

So how do you determine whether or not a graph is continuous?
First off, it has to follow three guidelines:

1. It has to have an existing limit for any value a.
2. The function has to have a value when x=a.
3. The limit and value have to be equal for any value a.

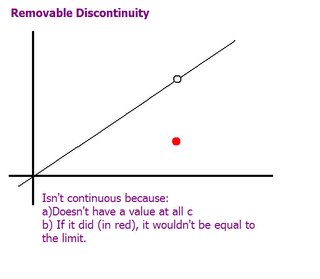
Removable discontinuities are basically those things they taught to us as "holes" in algebra.

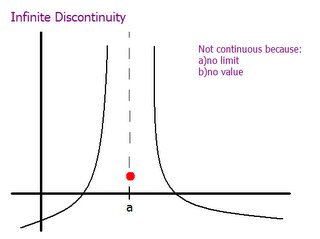
Infinite discontinuites basically have no limit for the value a.

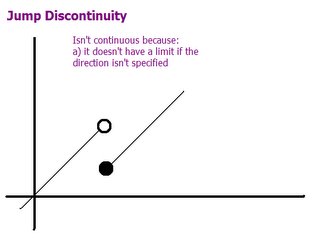
Jump discontinuities "jump" from value to value, like step functions.

Certain functions have domains which are all real numbers:

1. Polynomials
2. Trigonometric (only sin and cos)
3. Inverse Trigonometric (only tan-1 and cot-1)
4. Exponential
5. Roots (only odd ones)

Other functions have special domains:

1. Rationals
2. Trigonometry (only tan)
3. Inverse Trigonometric (only sin-1, cos-1, sec-1, and cosec-1)
4. Logarithmic

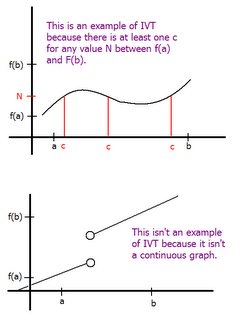
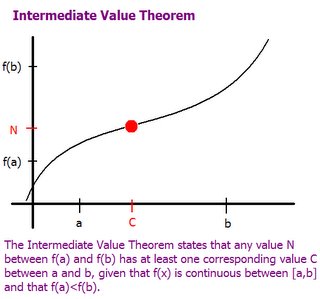
Intermediate Value Theorem (IVT)

Here's a link to another site with information on Continuity, though it has some extra info that isn't taught in our book:

http://www.sosmath.com/calculus/limcon/limcon05/limcon05.html

And here are some continuity problems:

http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/continuitydirectory/Continuity.html

And now for a photo I took while in New York this summer...

Reminder to JOEY to blog Monday's class notes!!

I'm out.