2.9 The Derivative as a Function

We have a few definitions for derivative. One is:

f ' (a) = limh→0 ((f(a + h) – f(a))/ h).

This gives the derivative for a specific value of a. However, we can generalize this definition to include any value of a. We use the variable x in place of a:

f ' (x) = limh→0 ((f(x + h) – f(x)) / h).

Here is an example:

f(x) = x^3 - x. Find the formula for f ' (x).

f ' (x) = limh→0 (((x + h)^3 - (x + h)) - (x^3 - x))/h
= limh→0 ((x^3 + 3x^2h + 3xh^2 + h^3 -x - h) - x^3 + x)/h
= limh→0 (3x^2 + 3xh + h^2 - 1)
= 3x^2 - 1
We can call the answer the general rule for the slope of tangent lines to f(x). Graphing the answer would give you a graph of the values of the slopes of the tangent lines to f(x).


Differentiable vs. Not:

There are many notations for the derivative. They include:

f '(x) = y' = dy/dx = df/dx = (d/dx)f(x) = Df(x) = Dxf(x). The D's and d/dx's indicate the operation of differentiation. A function is differentiable if we can find the derivative at a specific point or over a specific interval. Furthermore, if a function is differentiable on an interval, then it is continuous on that interval.

Here are some examples of functions that are not differentiable at certain points. If a graph has a corner (a kink or cusp), a discontinuity, or a vertical tangent at a, then the function is not differentiable at a.









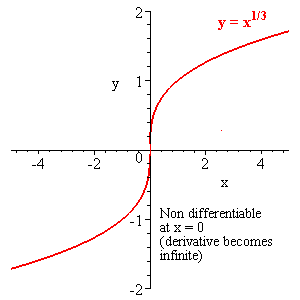
Not differentiable at x=0
(graph has a discontinuity).






Here is one link that has some good sample problems for f ' (x) problems. It shows you how to do them too: http://archives.math.utk.edu/visual.calculus/2/definition.12/. Below those examples is a different interpretation of differentiation.
Here is a differentiation link: http://www.people.hofstra.edu/faculty/Stefan_Waner/RealWorld/calctopic1/contanddiffb.html

Some good quotes:

The whole problem with the world is that fools and fanatics are always so certain of themselves, but wiser people so full of doubts.
Bertrand Russell

Whenever you find that you are on the side of the majority, it is time to reform.
Mark Twain

Look at all the sentences which seem true and question them.
David Reisman

The ultimate measure of a man is not where he stands in moments of comfort and convenience, but where he stands at times of challenge and controversy.
Martin Luther King, Jr.

RYAN, you are next.