4.6 Graphing with Calculus and Calculators

The main point of this section is that when plotting a graph using a calculator, the calculator can often be misleading. If the equation of a graph is highly complicated, the calculator can miss many important parts of the graph of the equation, such as extreme points. In order to fix this, you can adjust the window settings on the calculator to give you a better view of the graph. By using the first and second derivative, you can find the extreme points, the intervals of increase or decrease, inflection points, and the concavity of the graph. These values can help you determine a more appropriate viewing window for the graph.

For example:
Produce graphs of the above equation that reveal all the important aspects of the curve.

When you first graph the equation, you will probably get something like this by using ZoomFit on the calculator:


This graph does not reveal very much about the significant aspects of the curve. A more appropriate viewing window is needed. To make this process easier, find the first derivative.



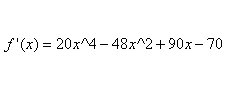
Now find the extreme points. You can use the graph of the derivative to find them:


The extreme points are (-2.255,) and (1.098,)



Based on this, the intervals of increase are:

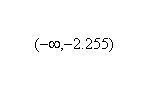
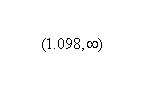
while the interval of decrease is: (-2.255,1.098)

In order to find the concavity and points of inflection, first find the second derivative.



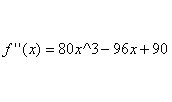
Now find the points of inflection. It is easy to do this by graphing the second derivative:


There is only one point of inflection, which is at (-1.4128,)

The graph of f(x) is concave up during:

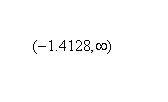
and concave down during:

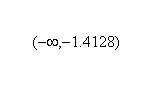
From this information we can find a more appropriate view of the graph.



Thus this is a more appropriate view of the graph. The y-window is [-500,500]. The x-window is [-5,5]

Here is a link to a website that can help you with this topic: www2.edc.org/cme/showcase/KY/calcliesarticle.pdf

This site applies this topic, but uses sinusoids rather than polynomials. Otherwise it is the same thing as this section.

Isaac, you are next to post, since Luke is no longer here.

Now, to finish things up, here is a comic. Hopefully, the AP exam will not be like this: