Section 4.4 Indeterminate Forms and L' Hospital's Rule

Alright so hopefully that comic got you ready for this section. Because it's on how you can get limits for infinities and zeros.

And just a heads up this blog is going to be slightly messy because I don’t have Equation Editor on my computer.

So first off, L’Hospital’s rule says that:

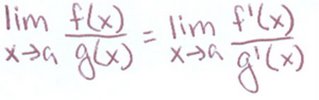
or, verbally, the derivative of a function f at point c is the same as the function itself if the function’s limit is equal to either zero or positive or negative infinity.

An example would be the equation we used in class

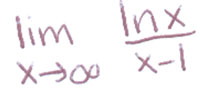
To find the limit, you need to plug in infinity for x.

We can see that it equals infinity over infinity, which is a indeterminate form. However using L’ Hospital’s rule, we can take the derivative of the function and start again. Thus, we can take the derivative of the function.

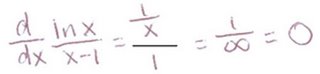
The derivative comes out to be 1over x. Then if you plug in inifinity, it is obvious that it nears 0. Thus the limit is zero.

Another problem is:

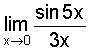
It's solution:

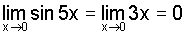
And how we can apply L'Hospital's Rule:


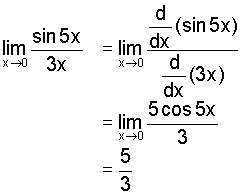
(taken from http://archives.math.utk.edu/visual.calculus/3/lhospital.1/index.html )

And now moving on to the other indeterminate forms. There are seven total that you need to know. The first two have already been mentioned: infinity over infinity and zero over zero. Those are called the indeterminate quotients. The indeterminate product is zero times infinity. The indeterminate difference is infinity minus infinity. The three indeterminate powers are zero to zero, infinity to zero, and one to infinity. In these equations infinity means a really really big number, 0 means a really really small number, and one means...one.

Here are some good sites if you are still confused after my amazing blog:
http://www.sosmath.com/calculus/indforms/otherquotient/otherquotient.html
http://archives.math.utk.edu/visual.calculus/3/lhospital.2/ (These are more problems if you want to test your self some more on L'Hospital's Rule)

Reminder to JOEY to post tomorrow’s notes!