Chapter 4.2
Today we discussed Rolle's Theorem and the Mean Value Theorem.
Let's start with Rolle's Theorem!
Rolle's Theorem is applicable if the following three conditions are true:
1.) f(x) is continuous on a closed interval [a,b]
2.) f(x) is differentiable on an open interval (a,b)
3.) f(a)=f(b)
(Note: In these conditions, f(x) is the function and a and b are points on the function)
Basically, Rolle's Theorem states that somewhere between points a and b on the graph of a function f, there exists a third point c that will have a slope of zero. This means that somewhere in between points a and b there is at least one maximum or minimum in the graph. A third way of saying this is that somewhere in between points a and b, there is at least one point that has a horizontal tangent.
Here is a basic graph that demonstrates the main idea of Rolle's Theorem:
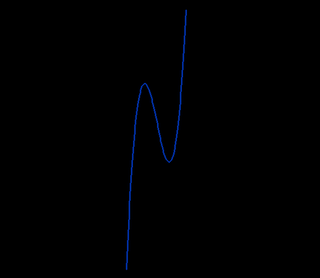
As you can see in this graph, all three of the conditions of Rolle's Theorem exist, and, as the theorem states, there is at least point(in this case there are two) in between points a and b that has a slope of zero and whose tangent is horizontal.
Here are some examples of cases in which the conditions of Rolle's Theorem break down:
Condition that breaks down: f(a)=f(b)
 As you can see, there is no value c in between a and b whose slope is zero.
As you can see, there is no value c in between a and b whose slope is zero.Condition that breaks down: f(x) is differentiable on (a,b)

As you can see, at point c, the graph of f(x) is not differentiable, and thus point c does not have a slope of zero
Condition that breaks down: f(x) is continuous on closed interval [a,b]

As you can see, since the graph of f is discontinuous, there is no point c in between points a and b with a horizontal tangent line.
Now Let's Review the Mean Value Theorem!:
In the Mean Value Theorem, the first two conditions of Rolle's Theorem hold true, but not the third, which states that f(a)=f(b). So, in order for the Mean Value Theorem to be applicable, f(x) must be continuous on the closed interval of [a,b] and f(x) must be differentiable on (a,b), but f(a) need not equal f(b).
Basically the Mean Value Theorem states that somewhere between points a and b on the graph of function f, there exists a point c whose tangent line has the same slope of the secant line between the end points.
Here is a geometric proof of the Median Value Theorem:


As you can see, the tangent line at point c, the red line, is parallel to the pink secant line between points a and b in the first graph, and that the tangent lines at point c1 and point c2 are parallel to the blue secant line from point a to point b in the second graph.(The first graph is accurate, while I had trouble making the lines in the second graph parallel, but you get the picture.) Basically, I was trying to portray that the Median Value Theorem is applicable in both scenarios.
Here are some helpful formulas for the Mean Value Theorem:
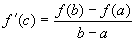
or

Here are some sample problems to help you understand these concepts better:
1.) Find the number, using the Mean Value Theorem, that satisfies this equation within the given domain:
Domain:

Solution: We will find this answer algebraically through a formula
First you must identify four things:
a=-1
b=3
f(a)=13
f(b)= 1
Then, you must plug these four pieces of information into one of the equations for the Mean Value Theorem:
We will use the equation:

When we plug in t
 he values for f(b), f(a), b, and a into this equation, we get:
he values for f(b), f(a), b, and a into this equation, we get:The next step is to find the derivative of f(x): which is 2x-5.
Now, we must set the derivative of f(x) equal to the derivative of f(c):
2x-5=-3
Once we solve for x, we have our answer!
2x=2
x=1
Don't forget to check to see if your answer lies in the given domain!
Since -1<1<3, our answer is correct.
2.) Suppose that f(0)=-7 and f'(x) <8 and >-3. How large and how small can f(3) possibly be?
Solution: We will also find this answer algebraically using a formula
First identify a,b,f(a), and f(b)
a=0
b=3
f(a)=-7
f(b)=?
To find the largest f(3) can possibly be, set the equation for the Mean Value Theorem equal to 8, which will be our f'(c), because we want to use the steepest slope possible to get the largest value for f(3).
For this problem, we will use the equation:

So, after plugging in
the appropriate n
 umbers into the equation, we get:
umbers into the equation, we get:So, the largest f(3) can be is 17.
To find the smallest f(3) can be, set the equation for the Mean Value Theorem equal to -3. In other words, f'(c) will be -3.
Solve this like the solution above, except substitute -3 for 8 for f'(c).
Our equation is:

So, the smallest f(3) can possibly be is -16.
Here are some additional sites to help you understand Rolle's Theorem and the Mean Value Theorem:
http://images.google.com/imgres?imgurl=http://www.math.hmc.edu/calculus/tutorials/mean_value/images/figure4.gif&imgrefurl=http://www.math.hmc.edu/calculus/tutorials/mean_value/&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;h=150&w=232&sz=1&hl=en&start=10&tbnid=mJniiUezf4BBIM:&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;tbnh=70&tbnw=109&prev=/images%3Fq%3DRolle%2527s%2BTheorem%26svnum%3D10%26hl%3Den%26lr%3D%26safe%3Doff%26rls%3DHPIC,HPIC:2005-19,HPIC:en%26sa%3DN
http://www.sosmath.com/calculus/diff/der11/der11.html
http://www.math.hmc.edu/calculus/tutorials/mean_value/
http://www.maths.abdn.ac.uk/~igc/tch/ma2001/notes/node42.html
This is an official reminder that JESSICA is posting next!
Here are a couple of calculus songs to get you into the upcoming holiday spirit and one song that I thought was funny!
" OH CALCULUS, OH CALCULUS!"
By Denis Gannon (1940-1991) may be sung to "Oh, Christmas Tree"
Oh, Calculus; Oh, Calculus,
How tough are your two branches.
Oh, Calculus; Oh, Calculus,
To pass, what are my chances?
Derivatives, I cannot take,
At integrals my fingers shake.
Oh, Calculus; Oh, Calculus,
How tough are your two branches.
Oh, Calculus; Oh, Calculus,
Your theorems I can't master.
Oh, Calculus; Oh, Calculus,
My proofs are a disaster.
You pull a trick out of the air,
Or find a reason, God knows where.
Oh, Calculus; Oh, Calculus,
Your theorems I can't master.
Oh, Calculus; Oh, Calculus,
Your problems do distress me.
Oh, Calculus; Oh, Calculus,
Related rates depress me.
I cut out boxes in my sleep,
And max and min do make me weep.
Oh, Calculus; Oh, Calculus,
Your problems do distress me.
Oh, Calculus; Oh, Calculus,
My limit I am reaching.
Oh, Calculus; Oh, Calculus,
For mercy, I'm beseeching.
My grades do not approach a B,
They're just an epsilon from D.
Oh, Calculus; Oh, Calculus,
My limit I am reaching.
Calculus
A Calculus Christmas Carol
written by Deborah Alterman, Martin Mohlenkamp, and Gareth Roberts (Sung to the tune of Jingle Bells)
Looking for the tangent
It's really m we seek
With epsilon and delta
Mathematics looks like Greek
Trying to find a limit
Everything gets small
If you can't determine it
You land in L'Hopital
Calculus, Calculus
Let us celebrate
Riemann Sums, so much fun
We can integrate
Calculus, Calculus
Let us celebrate
dx, dy, dz, dt
We love related rates
Calc 2 is coming next
The really fun stuff starts
Integral x sin(x)
Only works in parts
Summing the series harmonic
The terms keep getting small
But isn't it ironic?
It won't converge at all
Calculus, Calculus
Put your mind at rest
Most divergent series fail
The Root or Ratio Test
Calculus, Calculus
While we sing this song
We can sum (1/2)n
It won't take all day long
Now on to Calc 3
Learning spheres and cones
Maximizing functions
With seventeen unknowns
Fancy vector fields
Finding flux of curl
Using Mr. Stokes
Over a circle
Calculus, Calculus
Ain't it really cool
Gauss and Green are really keen
Don't take them for fools
Calculus, Calculus
Ain't it really cool
f and g, composing thee
Time for the chain rule

1 Comments:
You are such a goofball. I love it.
Post a Comment
<< Home