6.5: Average Value of a Function

Hey guys! Hey Mr. French! I hope you are all having a great Tuesday, I know I am. Anyways, let's get into the lesson. This lesson deals with the definition of an Integral: An approximation of the area bewteen the given curve and the x-axis between two given points. Now let's look at an example. We want to find the area under this cubic function, F(X).

Graph

Ok, now we want to find all the area bewteen the curve and the x-axis between the points a and b. Let's look at a visual depiction of that:
























Now we want to find this area using one large rectangle. Now of course a rectange is stright on all sides, so this area is going to be an approximation. We want to draw the rectangle so the area that it extends past the graph seems to be close to the area that is fails to cover in the graph. This will make more sense when looked at graphically. Let's look at that right now!






















So, as we can see the rectangle extends above the graph but fails to fill in certain areas under the graph. These areas cancel each other out. We are left with a close approximation of the area under the graph. Remember that any part of the graph below the x-axis represents negative area.


Now that we have looked at this visually, we can look at it in terms of an equation. We have just visually depicted the mean value theorem. The mean value theorem can be expressed mathematically as:





a and b are our boundaries and c is a point between a and b. f(c) is the avaerage value of the integral.

Now let's solve the equation for f(c):






Ok, now let's look at an example of this numerically....




We have the equation y=x+x2 [-1,2]


We don't actually need to graph it. We can use our equation for the mean value theorem.



a is -1, b is 2, and f(x) is x+x^2, so let's put that into our equation: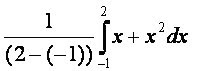







Now, let's simplify it further....








Next we use the rules of integration to take the antiderivative of the equation...







And lastly, we plug our a and b values (-1 and 2 into the antiderivative equation)...



1.5


1.5 is our "c" value, which is a point between a and b that lies on the graph. Now to find f(c), the average value, we solve our F(x) equation for x, setting it equal to our c value.

x+x^2=1.5.

When we solve this with the quadratic formula, we find that x= .823 and -1.823. Only .823 is within the boundaries, so that is our actual c-value.


Here is a good site about about the average value of a function: http://www.mathwords.com/a/average_value_function.htm. It's short, but i think it shows the concept clearly.




Also, before I go, I wanted to share with you an inspiration quote





"If A is sucess in life, then A equals X+Y+Z. Work is X, Y is play, and Z is keeping your motuh shut"- Albert Einstein

Here's a nice picture for all of you:


Since the order is now random, I have no one to remind. I'm out.