5.4 Indefinite Integrals and the Net Change Theorem

INDEFINITE INTEGRALS
An indefinite integral is basically the antiderivative of the function. It doesn't have upper and lower bounds because that would make it a definite integral. Indefinite integrals need the +C!

Table of Indefinite Integrals














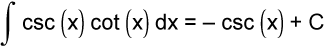
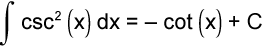
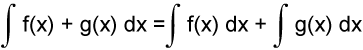
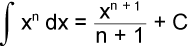
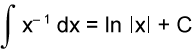
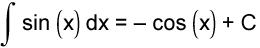
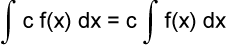
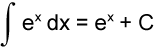
Sample Problem
Find the general indefinite integral



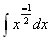
Using the formula:





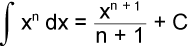
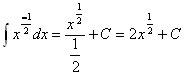
THE NET CHANGE THEOREM

The Integral of a rate of change is the net change (displacement for position functions)




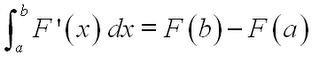
Basically this theorem states that the integral of f or F' from a to b is the area between a and b or the difference in area from the postion of F(a) to F(b).

This can be applied to things such as:
volume
concentration
density
population
cost
velocity

So for a velocity function:
To calculate displacement we can u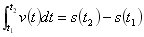se the equation



to calculate total distance traveled we can add the absolute values of the areas of each sector from each x int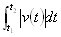ercept to the next x intercept



Sample Problem
A particle moves along a line so that its velocity at time t is

(m/s)

a) find the displacement from t=[1,4]
b) find the distance traveled during that time period

Finding the displacement:






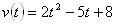
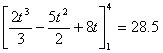
m.


Finding the total distance traveled during that time period


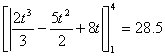
m.


The total distance traveled and the displacement are the same because the position function does not pass below the x axis therefore there are no negative areas. If there were negative areas the displacement would be a smaller number and the distance would stay the same.

Some LINKS:
http://www.coolschool.ca/lor/CALC12/unit5/U05L04.htm

A Lesser Lesson in Indefinite Integrals but helpful nontheless

Magnus You're Up NeXT!!!