Chapter 3 Test: Number 8

#8.)






In order to find the derivative of this function, the quotient rule must be used. The quotient rule is:






Another way to remember the quotient rule is by the following phrase: Low d high minus high d low all over the square of what’s below.

Thus, we will begin solving the problem by first identifying what the derivatives of the top(high) and the derivative of the bottom(low) are.

To find the derivative of the top: The derivative of the top is 1 because u can also be written as:

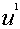
, and according to the power rule the derivative of x, or in this case, u, raised to
a number is equal to the number, in this case 1, multiplied by x, in this case u, raised to a number that is one less than the original exponent, in this case the new exponent will be 0 because 1-1=0. Thus,




So the derivative of the top is 1.

To find the derivative of the bottom: The derivative of the bottom can be found using both the product rule and the difference rule. We use the product rule, expressed above, to find the derivative of


.
So we have

,

or 2u, as the derivative of the first term of the denominator. The second term in the denominator is 1. According to the derivative of a constant function, the derivative of a constant is always 0. Since the number one is a constant, its derivative is 0. Now, we can use the difference rule to find the overall derivative of the bottom of the function. The difference rule basically states that you can find the derivative of the difference of two numbers by finding the derivatives of each individual number and then subtracting the derivative of the second number from the derivative of the first number. In this case, we take the derivative of the second number, 0, and subtract it from the derivative of the first number, 2u, and we get 2u-0, or 2u as the overall derivative of the denominator of the function.

To find the overall derivative of f(u):
Now, we can use the quotient rule to find the overall derivative of the function.
1.) Take the bottom and multiply is by the derivative of the top:




2.) Now take the top and multiply it by the derivative of the bottom: u(2u)
3.) Next, subtract step 2 from step 1:



4.) Square the bottom:



5.) Divide the numerator(low d high minus high d low), or step 3, by the square of the bottom, step 4:





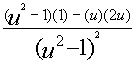
Thus, 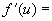as our answer, we have