Chapter 3 Test, #13

1. First, I started by setting up a diagram of this situation:



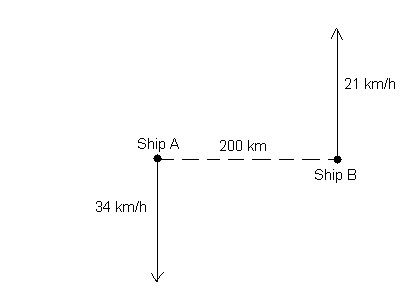
2. I then saw that from this diagram, I could create a triangle that looked like the following, with the hypotenuse c being the distance between the two ships:



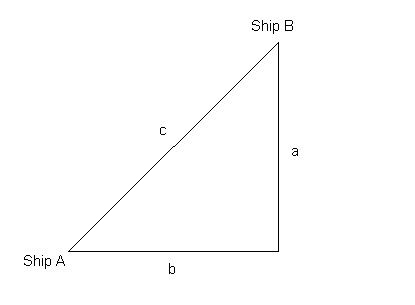
3. I then started to assign numerical values to each of the sides. We are given no value for c, so I left it as c. For b, we have the value of 200 km, which is the horizontal distance between the two starting points of the ships. To find a, I calculated how far each ship travelled by multiplying each of the ships' speeds by 8, because both ships were sailing for 8 hours.

Ship A=(34 km/h) * (8 h)=272 km
Ship B=(21 km/h) * (8 h)=168 km

Then, I added the two distances of Ships A and B, which equals 440 km, and I assigned that value to side a.

4. To find c, we can use the Pythagorean theorem:



We plug in the numbers that we assigned to a and b, and get the following equation to solve for c:



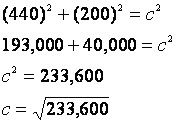
We will also use the Pythagorean theorem for our static equation.

5. Now we have to change the static equation into a dynamic equation by differentiating both sides of the equation. If we differentiate the Pythagorean theorem, we get the following dynamic equation:



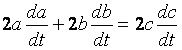
6. Now, we plug in the values that we have, solving for dc/dt

a=440
b=200
c=(233,600)^(1/2)
da/dt=rate of ship A+rate of ship B=55
db/dt=0 (b is our constant)
dc/dt=unknown



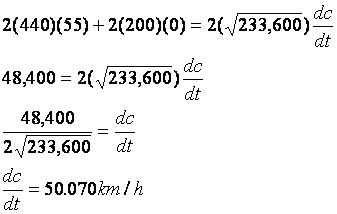
The answer to the problem, rounding to the nearest thousandth, is 50.070 km/h