3.7 Higher Derivatives

In today’s lesson, we learned that not only can you take a derivative of a function, you can take the derivative of another derivative as well!!! Let’s take a look:

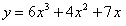
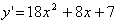(As usual, we are finding the derivative of the first equation)
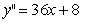(However, we can also find the derivative of the first derivative which is called double primes)
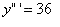(We can even find the derivative again of double prime and make it triple prime)
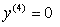(And lastly you can find the fourth prime which in this case is the final derivative possible since you have reached 0!)


Let’s look at some new notation we learned today that might be on the quiz/test/AAAPPP!!!!!

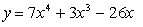
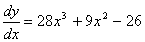(Now this derivative is finding the slope of the tangent line/ instantaneous rate of change)
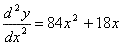(This shows how the derivative is changing)
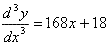(This shows how the previous derivative is changing as well)


You can also use the concept of Higher Derivatives on the Trigonometric Functions





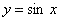
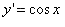
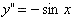
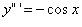
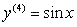
As you can see, the 4th prime equation is back to (sinx). This means that every fourth derivative in this situation repeats. Therefore could you find ?

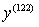If you divide 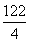, you will get 30 remainder 2. Thus you look at your double prime which is the second equation and you see that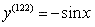


Now let’s use this concept on an exponential function:




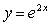
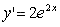
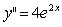
How about ?


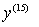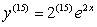
Finally why don’t you try a velocity/ acceleration problem which incorporates the higher derivative concept. If the function 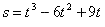is given for the position of a particle, find:
1) Acceleration at time t. What is the acceleration after 4 sec?
2) When is the particle speeding up and slowing down? Show this through a graph for
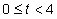
Velocity function(derivative of the position function):
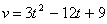
Acceleration function (derivative of the velocity function) :
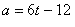
For the acceleration after 4 s, just plug it into the previous equation.



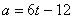
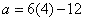
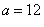
To find when the particle is speeding up and down, you must first equal the velocity function to 0.



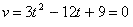
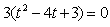
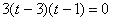
So at t=1 and 3, the particle is at rest.
Plug numbers in for t (in the equation 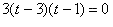) and you will see that if the particle was moving before t=1, the particle has positive velocity, if the particle was moving between t=1 and 3, the particle has negative velocity, and if the particle was moving after t=3, the particle would have positive velocity.

How about acceleration? Make the acceleration function=0:
a=6t-12
0=6t-12
t=2; meaning at 2 seconds, the particle will have 0 acceleration.
Before t=2, the acceleration will be negative and after t=2, the acceleration will be positive.

Therefore, when the signs of velocity and acceleration are the same, the particle is speeding up. If the signs are opposite then it means that the particle is slowing down.


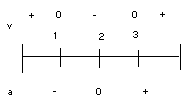
Speeding up:
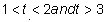
Slowing down:

For more perspective:
http://tutorial.math.lamar.edu/AllBrowsers/2413/HigherOrderDerivatives.asp

Brian - you're next!