Prep AB Calculus C 2006-07: 4.8: Applications to Business and Economics

Hey guys i hope you are all having a great weekend. I am in laguna right now writing this on the balcony overlooking the ocean, enjoying the warm breeze and sipping on a mango smoothie. Thought i would make you jealous. Anyway, let's get into it. 4.8 is all about applying derivatives to the business world.

Let's start off by defining some things, since a good portion of this section is about understanding business jargon. You will see that these business terms are simply real world applications of functions and derivatives of functions.

1) c(x) = the cost function. It is the cost of producing "x" amount of a certain product. The cost function tells us how much is spent in relation to how much is produced.

2) c'(x)= marginal cost. This is the derivative of the cost function. From what we learned before about expressing the meaning of a derivative verbally (how something is changing with respect to somethign else), we can say the marginal cost is the rate at which the cost is changing with respect to the number of units produced.

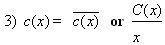= The average cost. This is the cost divided by the total number of units. Remember from 1) that the cost function is the cost of producing "x" amount of a certain product.

..Now because we are in calculus and examine derivatives, we are of course going to look at minimums and maximums, terms we are all familiar with. The term minimum average cost means that the the marginal cost, defined above as C'(x), or the derivative of the cost, = the average cost defined above as the cost function divided by the number of units produced, expressed in terms of "x".

In mathematic terms, minimum average cost=

4) p(x)= the price function. The price function represents the price per unit a company can charge if it sells "x" units.

5) R(x)= p(x) . x= revenue. Revenue is the product of the price, expressed as(p(x)) and the quantity, expressed as "x". Simply put revenue is the amount of money the company collects.

6) R'(x)= the marginal revenue function. Like the marginal cost function, this is simply the derivative of the revenue function. Once again we can use our prior knoweldge of the meaning of a derivative to verbally state that the marginal revenue is the instantaneous rate of change of revenue with respect to the number of units sold.

7) P(x)= R(x)-C(x)= the profit function. The proft function is the difference between the revenue function (see 5) and the cost function (see 1). RYAN'S WARNING: Note that the profit functuon is represented by a capital P, while price is is represented by a lowercase p.

8) P'(x)= R'(x)- C'(x)= the marginal profit function. P' is the derivative of the profit function (see 7), R'(x) is the derivative of the revenue function, or the marginal revenue (see 5 and 6), and C'(x) is the derivative of the cost function, or the marginal cost (see 1 and 2).

...Once again, because we are in calculus and are using derivatives, we are going to of course have to examine maximums and minimums (since these occur when a derivative equation is equivalent to zero) When marginal revenue equals marginal cost, profit is maximized, or when R'(x)= C'(x) (the dertivative of the revenue function equals the derivative of the cost function), profit is maximized.

Now that we have defined all these thick business terms and can see that if they are flowery terms for things that we all understand, like liner functions and derivatives of functions, let's see if we can do a problem..

Ryan Lamont, after mastering Calculus and no longer failing Mr. French's quizes, opens up a Calculus Art exhibit in which he draws the graphs of derivatives. He puts them on display so the the public can enjoy his masterpieces. He sells 600 tickets at $9 and predicts, through an intense study of current market trends, that if he drops the price to $7, he will sell 800 tickets. At what price should he charge for tickets to maximize his revenue?

ok, so first let's make an equation for the price function. The price function represents a linear relationship so we can use point slope form to make our equation...

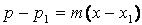
Now that we have made our equation, let's solve for m. We have two x values (600 and 800) and two p, or y values (9 and 7) so let's subtract the y's and divide the difference by the difference between the x's. Let's take the slope...

7-9/800-600= -2/200= -1/100= -.01. m= -.01.

Now, since we have two x values and two p values, we use one pair and substitute it into the eqaution with our newly found m also. Let's use ($7, 800).

So.. p-7= -.01(x-800).

Now let's distribute and isolate P by adding 7... p-7=-.01x+ 8. WHen we add 7, we get
p= -.01x+15

Now that we have our profit equation, we know that revenue equals the product of the profit equation and the quantity in terms of x (see 5). So, R(x)= p(x) . x. Since p(x)= -.01x+ 15, R(x)= (--.01x+15) (x), which equals -.01x^2+15x.

So, R(x)= -.01x^2+15x

Now that we have our revenue function, we want to take the derivative, which eauals the marginal revenue. So, using basic power rule properties, we come up with the equation:

R'=-.02x+15

Now, we want to set the derivative of the revenue function to zero, as we always do when finding maximums and minimums, and solve for x in the R' equation. So, we subtract 15 and divide by -.02.

-15/-.02= 750 so x=750.

We know that this x value maximizes our revenue. We can use the first derivative test and test values to the right and left of 750 on the number line, or we can use logic and realize that the graph of R is a parabola which opens downward. Now that we have proven this value gives us a maximum, our last step is to plug it back into the orginial price equation, p=-.01x+15.

...-.01(750)+15= 7.5, so our answer is $7.50. Pricing the tickets at $7.50 Ryan will maximize his revenue.

Ok well that is the end of the lesson.

Since the only new thing in this lesson was new terms ( all the actual calculus involved is review), i found a site that explains those business terms: http://ingrimayne.com/econ/MakeProfit/Overview10mi.html

There are also some great problems in here, not all of them are relevant to this section, but the ones that are are excellent: http://64.233.161.104/search?q=cache:0JHVsGpN1nwJ:www.math.mcgill.ca/~laayouni/Teaching/Math122/Lecture17.pdf+derivatives+calculus+maximize+cost&hl=en&gl=us&ct=clnk&cd=6 eaching/Math122/Lecture17.pdf+derivatives+calculus+maximize+cost&hl=en&gl=us&ct=clnk&cd=6

Before i go, i wanted to share with you an alliteration poem i wrote in 5th grade in Mrs. Rogers' class. For those of you who don't know, alliteration means using the same first letter multiple times in a sentence.

Here is my poem:

Royal Radical Ryan Rode Rough Rhinoceroses to Rhode Island While Ravishing Ruby Red Radishes.

I knew you would enjoy that.

This picture speaks for itself: