8.1 Arc Length

Okay, so it's finally my turn again~! I'm here to explain Chapter 8, Lesson 1, which is about finding arc lengths.

When a curve is a polygon, finding the length is easy because all you have to do is add up the sides but when you get a continuous curve, it gets tricky! Remember that a curve is defined by the equation y= f(x) where f is continuous on a (equal to or less than) x (equal to or less than) b. When we estimate the value of a curve, we are taking approximations as if the sides of a polygon were present in it. (page 547 in the textbook)

The length is described using the distance formula (as the limit approaches infinity). The distance formula is not practical to use with a smooth function, so we can derive an integral formula for L where the function has a continuous derivative, because there is only a very small change in f'(x). (Also think of the approximation as taking the Pythagorean theorem to find the hypotenuse with infinitely many tiny triangles, as described in class)

The arc length forumula for the curve y=f(x) where is a is (equal to or less than) x (equal to or less than) b

(if f' is continuous on [a,b])

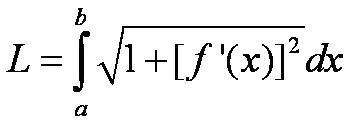
it can also be notated as:


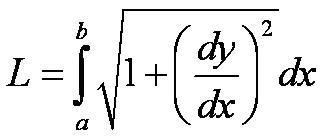
In the other case, if a curve has the equation x=g(y) with c (less than or equal to) y (less than or equal to) d, and g'(y) is continuous, we get this formula for arc length:




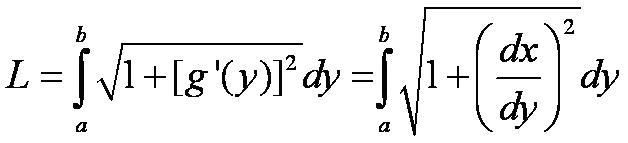
Keeping these two formulas in mind, let us try a problem!

If y=e^4x and 0 (less than or equal to) x (less than or equal to 1), find the arc length.

We begin by writing the integral, which will be from 0 to 1, and plug in the derivative. Remember to use the chain rule in this case, because the derivative of e^4x is 4(e^4x). Don't forget details such as chain or product rule when taking derivatives! Also remember to even TAKE the derivative, and to SQUARE it. But I digress. After setting everything up, it should look like this:



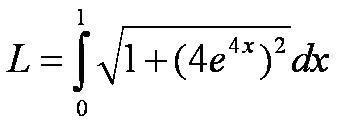
Afterwards, you can either figure out the antiderivative or if you are short on time or just wish for simplicity (in this case), plug it in to your calculator and do fnInt! Oh yeah, another minor detail. Don't forget to write "dx" when doing your problems, and don't get your dx's and dy's mixed. I think it's just me, but it's still a possible mistake.

...aaaannndddd here are a few links:

http://en.wikipedia.org/wiki/Arc_length (history teachers can scorn Wikipedia but this site gives a good explanation of this math concept, provided that no users/pranksters go edit it, but it always gets edited back anyhow)
http://tutorial.math.lamar.edu/AllBrowsers/2414/ArcLength.asp

http://www.math.hmc.edu/calculus/tutorials/arc_length/


and here's a funny little video for you all. just remember when you decide to bring your kitten in for show-and-tell, don't let it near Mr. French's laptop. (Has anyone posted it on the blog already? Remind me if anyone has)



carpe diem, everyone.

until next time~!

-Sonia

Oh yea, Crystal. You're up next xD