Section 3.3: Rates of Change in the Natural and Social Sciences

Section 3.3 explains to us how derivatives can connect with science and economics. We see in this section how useful it is to find the rate of change of functions in the natural and social sciences.





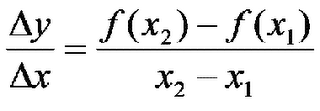
This is the slope of the secant line from x2 to x1. As x2 approaches x1 the secant line becomes a tangent line, giving us the instantaneous rate of change at that point. From this, the derivative can be defined as is below.

Average rate of change of y with respect to x:























The book explains the following areas of science that we can apply the derivative to.
Physics:
In physics, the derivative of s = f(t), where s is the position of an object moving in a straight line and t is the time, is the instantaneous velocity.

This is a schematic sketch of the motion of a particle moving back and forth along a line.












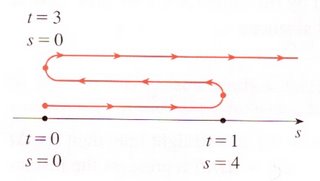
http://www.physics.upenn.edu/courses/gladney/mathphys/subsubsection2_1_1_2.html#SECTION02_1_1_2


Chemistry:
In chemistry, the derivative can be used to find the concentration of reactants during a chemical reaction. However, the derivative is often used to find the instantaneous rate of reaction. Compressibility is another area where we can apply the derivative.
http://www.physics.upenn.edu/courses/gladney/mathphys/subsection2_1_4.html
http://www.physics.upenn.edu/courses/gladney/mathphys/subsubsection2_1_1_4.html#SECTION02_1_1_4


Biology:
In biology, we can find the instantaneous rate of growth and velocity gradient. Also, the flow of blood in a blood vessel can be analyzed using the derivative.
http://www.physics.upenn.edu/courses/gladney/mathphys/subsection2_1_2.html#SECTION02_1_2

Economics:
In economics, we can find the instantaneous rate of change of cost, or the marginal cost.

When C is the cost, the marginal cost can be found using the derivative.








Of course, the derivative can be used in many more sciences other than these ones.

Sample:
A particle moves according to a law of motion s = f(t), t > 0, where t is measured in seconds and s in feet.





a.) Find the velocity at time t
b.) What is the velocity after 3 s?
c.) When is the particle at rest?
d.) When is the particle moving in the positive direction?
e.) Find the total distance traveled during the first 8 s.

Solution:
a.) First, we find the derivative of the function.





b.) Then plug in 3 into the derivative function to get:
-9 ft/s

c.) We find the zeroes of the derivative function by either graphing or using the quadratic equation and find that:

Zeroes: x=2, x=6

d.) We find the intervals where the derivative function is positive and we get
0<t<2,>6

e.) This one is a little harder. We have to take in account of when the object is moving backwards. When the derivative function is negative, the object is doing so which is between 2 seconds and 6 seconds.

Then, we plug in the times in the original function.

i.) During the first 2 seconds the object travels 128 ft.
ii.) Then it goes backward between seconds 2 and 6, moving -736 ft.
iii.) Finally it goes forward again after 6 seconds. Between seconds 6 and 8, the object travels 704 ft.

Adding all of these together, we figure out the object’s displacement is 96 ft.

“Respect yourself and others will respect you.”
- Confucius

Reminder to Claire for next blog!