Section 3.4: Derivatives of Trigonometric Functions

So we've been taking the derivatives of functions for a while now, and I know that a question that's been burning in everyone's mind is if we can take the derivatives of trigonometric functions. Well, the answer is finally here, and of course we can. Just take a look at this graph of sin x.

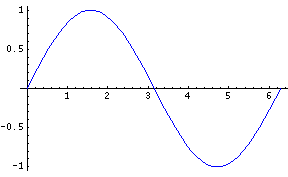
If you take the derivative of this graph, it comes out looking something like this:

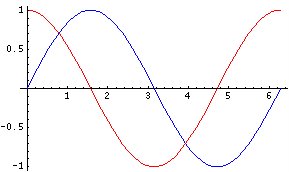
Holy Cow! It kinda looks like the graph of cos x! Imagine that. I'm in shock.

Wait a second, what happens if we draw the derivative of cos x?

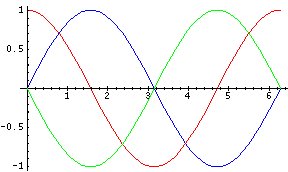
Looks sorta like the sin x graph only flipped. Maybe it's the -sin x graph. No way!

So:

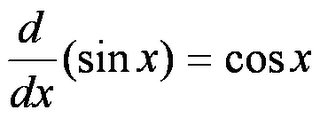
and

But there's more! By using a similar way of finding the derivative, you can find that:

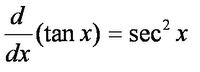
and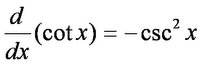 So let's do a problem!

If you want to see the algebraic proofs for this lesson, or if you just need some help understanding the concept, you can check out this website.

http://archives.math.utk.edu/visual.calculus/2/trig.1/index.html

Oh, and I found someone that actually solved the sudoku that was on our test the other day...

P.S. -Reminder to Ismael