5.3 The Fundamental Theorem of Calculus

Hey guys this is Izzy. Today in class we learned about the fundamental theorem of calculus. This theorem establishes a connection between the two branches of calculus: differential calculus and integral calculus. In class we covered how if you multiply the function that you are taking the integral of by a certain factor, that you can factor out that number. Example:

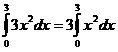
This makes it easier to deal with the original funtion first, without any coefficients to clutter up the process.

In class, we saw how the integral of a function can be a function itself, represented by g(x). Expressing the integral of a function as the function g(x) allows one to actually graph and express the area between the curve of a graph and the x-axis in terms of x:

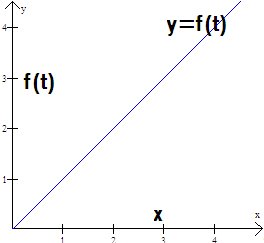
In this graph,

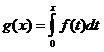
By using this equation, we can find the area between the graph and the x-axis. Let's say we wanted to find the area between x=0 and x=3. You would multiply the change in x, 3, by f(3), 3, and .5, because it's a triangle. So, g(3)=(3)(3)(.5)=4.5 .



Today we also made the amazing discovery that the antiderivative of a function is the same as the integral of the function. Observe:


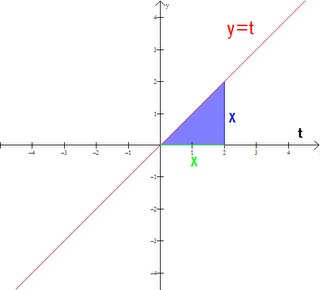
As you can see from the graph, the area of the shaded region (teal) is:



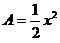
We established that

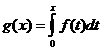
To find g'(x), we have to replace t with x and multiply whatever you get by the derivative of x.

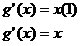
Wait a minute, the derivative of the Area function is also x! Thus A'=g'(x). We just proved that the antiderivative of a function is the same as its integral! i'm so happy.

What we just did relates to the Fundamental theorem of Calculus, Part 1, which states that:
If the function f is continuous on [a,b], then the function g defined by

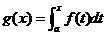
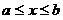
is continuous on [a,b] and differentiable on (a,b), and g'(x)=f(x)

MOVING ON, we now know how to find the derivative of these types of functions. Let's try this problem: Find

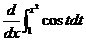
Whenever you see these types of problems, you must first look at the upper bound, or any of the bounds that has a variable in it. In the process of calculating the equation for g'(x), you must replace the variable t with the variable bound, and wherever you see dt, replace it with the derivative of the variable bound. In this case, the upper bound has the variable: x^2.
To solve this problem, we have to use the chain rule (make u=x^2):


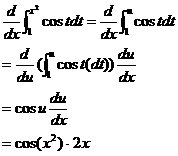
There you have it.


This a reminder to Ami to do the next blog!

These are a few websites that help out with this concept:

http://www.ugrad.math.ubc.ca/coursedoc/math101/notes/integration/ftc.html
http://archives.math.utk.edu/visual.calculus/4/ftc.9/

Here are some cool math jokes
Q: What do you get if you divide the cirucmference of a jack-o-lantern by its diameter?
A: Pumpkin Pi!

Q: Why do you rarely find mathematicians spending time at the beach? A: Because they have sine and cosine to get a tan and don't need the sun!

A mathematician is flying non-stop from Edmonton to Frankfurt with AirTransat. The scheduled flying time is nine hours. Some time after taking off, the pilot announces that one engine had to be turned off due to mechanical failure: "Don't worry - we're safe. The only noticeable effect this will have for us is that our total flying time will be ten hours instead of nine." A few hours into the flight, the pilot informs the passengers that another engine had to be turned off due to mechanical failure: "But don't worry - we're still safe. Only our flying time will go up to twelve hours." Some time later, a third engine fails and has to be turned off. But the pilot reassures the passengers: "Don't worry - even with one engine, we're still perfectly safe. It just means that it will take sixteen hours total for this plane to arrive in Frankfurt." The mathematician remarks to his fellow passengers: "If the last engine breaks down, too, then we'll be in the air for twenty-four hours altogether!"

A math student is pestered by a classmate who wants to copy his homework assignment. The student hesitates, not only because he thinks it's wrong, but also because he doesn't want to be sanctioned for aiding and abetting. His classmate calms him down: "Nobody will be able to trace my homework to you: I'll be changing the names of all the constants and variables: a to b, x to y, and so on." Not quite convinced, but eager to be left alone, the student hands his completed assignment to the classmate for copying. After the deadline, the student asks: "Did you really change the names of all the variables?" "Sure!" the classmate replies. "When you called a function f, I called it g; when you called a variable x, I renamed it to y; and when you were writing about the log of x+1, I called it the timber of x+1..."