3.6 Implicit Differentiation

Hey guys, this is Ismael if you hadn’t already guessed. Today we learned about implicit differentiation. Implicit differentiation is different from explicit differentiation in that the explicit functions we have dealt with so far only deal with expressing one variable explicitly in terms of another variable. Implicit functions express the relationship between y and x implicitly. For example:

Explicit


Implicit


The implicit equations can be used to draw the graph of a circle. By solving
for y you get .The function is the upper half of the circle and the function is the lower half of the circle. Graphing this function gives us:


The tangent lines represent the derivatives of both functions when x=5.

You can differentiate implicit functions like these by this method:


Use the Chain Rule:
This is the same thing as saying 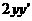because y=f(x) and 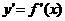. Therefore:


Here is an example of this method of using implicit differentiation to find y' (the slope):

Note: because we are not dealing with x in this case; we are dealing with y, which represents a function. Therefore, it is necessary to take the extra step of taking the derivative of the inside function, which is y. As a result .

Let's continue:


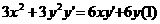
Now move over the 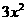and the 6xy' terms to the opposite sides of the equation so that they switch places.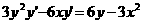

This allows us to factor out y prime


Now we know the slope of the function. Let’s say we had to find the slope of the implicit function at the point (3, 3). We would simply plug in x=3 and y=3 into the equation we derived for y'.

Use the point slope formula:

Let’s say we were to find the points on the graph at which the slope of the tangent line was 0. First, you would set the equation for y' equal to 0.

Now we plug what we got for y into the original equation.


Bring to the other side of the equation: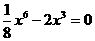


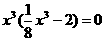
Now we think: for what values of x would the left side of the equation equal zero? One value, obviously, it would be x=0. To find the second one, we first divide both sides by , giving us: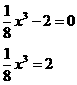

We then multiply both sides of the equation by eight and get:

Therefore, the values at which the derivative of the graph is zero are and x=0. To find the y values, simply plug in the x values into the equation .

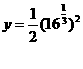
Therefore, the points on the graph at which the tangent line is horizontal to the curve are: (0,0) and ,.

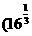Now, we move on to inverse trig functions!
Let’s say we have
That equation is the equivalent of
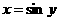
By implicit differentiation:



By using our Pythagorean rule for the relationship between sine and cosine
( ) we can come up with:



(Note: We can replace with because of our original equation: )


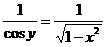
Therefore,

You can look at page 233 in our text book for the table of all of the derivatives of the inverse trigonometric functions.

By the way, Ami, you are next for the blog posting.

Here are a couple of links supporting the Topic of the Day:
http://archives.math.utk.edu/visual.calculus/3/implicit.7/index.html

http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/implicitdiffdirectory/ImplicitDiff.html

And to end this blog with a bang, here are a few Ben Franklin quotes:

"Anger is never without reason, but seldom a good one"

"Do not fear mistakes. You will know failure. Continue to reach out."

"Either write something worth reading or do something worth writing."

"Employ thy time well, if thou meanest to gain leisure."

"Experience is a dear teacher, but fools will learn at no other."

And some silly quotes:

"Sure there have been injuries and deaths in boxing - but none of them serious." - Alan Minter, Boxer

"I think that the film Clueless was very deep. I think it was deep in the way that it was very light. I think lightness has to come from a very deep place if it's true lightness." - Alicia Silverstone, Actress

"How to store your baby walker: First, remove baby." - Anonymous Manufacturer

"You guys line up alphabetically by height." - Bill Peterson, Florida State football coach

"Men, I want you just thinking of one word all season. One word and one word only: Super Bowl." - Bill Peterson, football coach

"The internet is a great way to get on the net." - Bob Dole, Republican presidential candidate