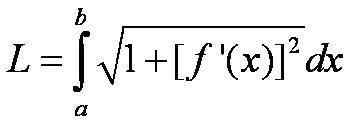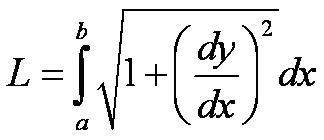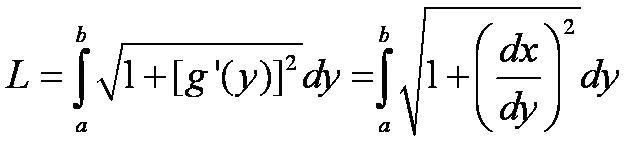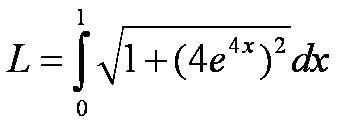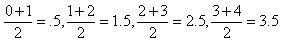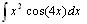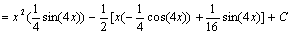9.1 Modeling with Differential Equations

The second formula we were taught is dubbed the Rate of Growth for a Population-bounded on our concept sheets. It is:

This equation is also the derivative of a logistic function. It expresses the fact that when we have a small population, the population will grow quickly. But as the population approaches the carrying capacity, it won't be able to grow so quickly and will level off. If P/K were to ever become greater then 1, then the population would start to decline.
The next thing we learned about was the IVP, or the Initial Value Problem. The two steps to these situations are:
1. Solve the differential equation for a general solution.
2. Use the general solution and data point to solve for a specific solution.
For example:
Given  and the point y(0)=5, find the IVP.
and the point y(0)=5, find the IVP.

http://www.math.ohiou.edu/~ashish/h13.pdf That's a nice quick summary straight from our book that Ohio University made.
http://www.mathsci.appstate.edu/~hph/3310/diffeqn/ This site has examples of different kinds of differential situations.
Alex, you get the blog next =D
My favorite quote for the past month has been "You smell funny" from POTC:DMC.
And now for some lame math jokes...
Q: What is the first derivative of a cow?
A: Prime Rib!
Q: What caused the big bang?
A: God divided by zero. Oops!
"A mathematician is a blind man in a dark room looking for a black cat which isn't there."- Charles Darwin
and for my last few words:
A guy gets on a bus and starts threatening everybody: "I'll integrate you! I'll differentiate you!" So everybody gets scared and runs away. Only one person stays. The guy comes up to him and says: "Aren't you scared, I'll integrate you, I'll differentiate you!" And the other guy says: "No, I am not scared, I am e^x."