In this section, we learned how to use information about  to give us information about
to give us information about  .
.
Increasing/Decreasing Test
Since  represents the slope of the curve
represents the slope of the curve  at the point
at the point  ,
,  tells us when the function is increasing or decreasing. The Mean Value Theorem we learned earlier leads to the conclusions:
tells us when the function is increasing or decreasing. The Mean Value Theorem we learned earlier leads to the conclusions:
1. When  is positive,
is positive,  is increasing.
is increasing.
2. When  is negative,
is negative,  is decreasing.
is decreasing.
We can use these two statements to test whether a function is increasing or decreasing based on the first derivative. Hence, the name “Increasing/Decreasing Test”.
The First Derivative Test
We can also use the first derivative to find the local maximum and minimum of the graph of the function.
We first find the critical numbers of the function. Critical numbers are the x-values in the domain of a function  when the derivative
when the derivative  is zero or undefined. To find the critical numbers, set
is zero or undefined. To find the critical numbers, set  and solve for x.
and solve for x.
Once the critical numbers have been found, determine whether each critical number is a local maximum, a local minimum, or neither. To do so, draw a number line, mark the number line  , and mark the critical numbers on the line.
, and mark the critical numbers on the line.
We know that  is equal to zero at the critical numbers. Using the number line, we can find the sign changes for each critical number. These sign changes determine the nature of each critical number. This is called the First Derivative Test:
is equal to zero at the critical numbers. Using the number line, we can find the sign changes for each critical number. These sign changes determine the nature of each critical number. This is called the First Derivative Test:
1. If the sign of  changes from positive to negative at a critical value, then
changes from positive to negative at a critical value, then  has a local maximum at that x-value.
has a local maximum at that x-value.
2. If the sign of  changes from negative to positive at a critical value, then
changes from negative to positive at a critical value, then  has a local minimum at that x-value.
has a local minimum at that x-value.
3. If  does not change sign at a critical value, then there is neither a local minimum nor a local maximum at that x-value.
does not change sign at a critical value, then there is neither a local minimum nor a local maximum at that x-value.
Example
For  , (a) Find the critical values & identify each as a local maximum, minimum, or neither. (b) State the intervals where
, (a) Find the critical values & identify each as a local maximum, minimum, or neither. (b) State the intervals where  is increasing.
is increasing.
Solution
Here is an example in which we use the Increasing/Decreasing Test and the First Derivative Test.
(a) 



Now that we have the critical values, we create a number line and plot those values.

Using the First Derivative Test, we conclude the following:
Since  changes from + to – at
changes from + to – at  ,
,  is a local maximum
is a local maximum
Since  changes from – to + at
changes from – to + at  ,
,  is a local minimum
is a local minimum
(b) Since is positive on the intervals to the left of -2 and to the right of 0, is increasing on the intervals  and
and  .
.
Concavity & The Second Derivative
The first derivative of a function helps determine the local maximum and minimum and also tells where the function is increasing or decreasing. The second derivative  tells us about the shape of the curve, its concavity, and also gives us the Concavity Test.
tells us about the shape of the curve, its concavity, and also gives us the Concavity Test.
Look at Curve #1 below. In the graph, the slopes of the tangent lines change from negative to zero to positive. Therefore, the slope of the tangent,  , is increasing. When a function is increasing, the derivative of
, is increasing. When a function is increasing, the derivative of  , that is
, that is  , is positive. This type of shape is concave up.
, is positive. This type of shape is concave up.

Look at Curve #2 below. In the graph, the slopes of the tangent lines change from positive to zero to negative. Therefore, the slope of the tangent,  , is decreasing. When a function is decreasing, the derivative of
, is decreasing. When a function is decreasing, the derivative of  , that is
, that is  , is negative. This type of shape is concave down.
, is negative. This type of shape is concave down.

In Curve #1, there is a local minimum. In Curve #2, there is a local maximum. This gives us the Second Derivative Test:
If c is a critical number of  , and
, and
 , then there is a local minimum at c.
, then there is a local minimum at c.
 , then there is a local maximum at c.
, then there is a local maximum at c.
The Second Derivative Test is easy to use, but it is also limiting because there is no conclusion when  . In that case, use the First Derivative Test, which can be applied in every case.
. In that case, use the First Derivative Test, which can be applied in every case.
Points of Inflection
Points of inflection are points where the concavity of a function changes. Points of inflection are at values in the domain of a function where  changes sign from positive to negative or from negative to positive.
changes sign from positive to negative or from negative to positive.
We find points of inflection in a way similar to finding critical numbers. First, find  of a function and solve for the x-values when
of a function and solve for the x-values when  is zero or undefined. These x-values are possible points of inflection. Next, draw a number line, mark the number line
is zero or undefined. These x-values are possible points of inflection. Next, draw a number line, mark the number line  , and mark the x-values on the number line. We know that
, and mark the x-values on the number line. We know that  at these possible points of inflection is zero or undefined. Using the number line, we can find the sign changes for each of these points. If
at these possible points of inflection is zero or undefined. Using the number line, we can find the sign changes for each of these points. If  changes sign around the x-values on the number line, then that x-value is a point of inflection.
changes sign around the x-values on the number line, then that x-value is a point of inflection.
Example: Let us find the points of inflection of  .
.
Solution:
We find the first derivative,  .
.
Then we find the second derivative,  .
.
Since  is never undefined for this function, find the points of inflection by solving:
is never undefined for this function, find the points of inflection by solving:



 changes from negative to positive around -1. Therefore, the point of inflection for
changes from negative to positive around -1. Therefore, the point of inflection for  is (-1, 6).
is (-1, 6).
Two links you can check out for further information:
http://www.math.hmc.edu/calculus/tutorials/extrema/
http://www.math.hmc.edu/calculus/tutorials/secondderiv/
Reminder: Crystal, you are up to post next.
Here are some pictures I took at the Huntington Gardens:







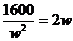
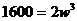
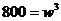





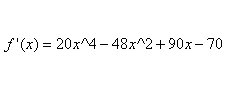

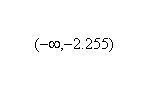
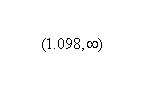
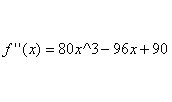

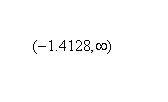
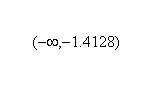






 to give us information about
to give us information about  .
.  at the point
at the point  ,
, 
 , (a) Find the critical values & identify each as a local maximum, minimum, or neither. (b) State the intervals where
, (a) Find the critical values & identify each as a local maximum, minimum, or neither. (b) State the intervals where 



 ,
,  is a local maximum
is a local maximum ,
,  is a local minimum
is a local minimum and
and  .
. tells us about the shape of the curve, its concavity, and also gives us the Concavity Test.
tells us about the shape of the curve, its concavity, and also gives us the Concavity Test.

 , then there is a local minimum at c.
, then there is a local minimum at c. , then there is a local maximum at c.
, then there is a local maximum at c. . In that case, use the First Derivative Test, which can be applied in every case.
. In that case, use the First Derivative Test, which can be applied in every case. .
. .
. .
.





