Section 6.1: Areas Between Curves

Yay it's my turn now. As I look at these problems more and more, they seem less scary, so if any of you are worried about this concept, as I was, don't worry because with some practice, I'm sure that you can kick these problems' butts! Before I get into summarizing this lesson, here is a link for any further information: http://tutorial.math.lamar.edu/AllBrowsers/2413/AreaBetweenCurves.asp

Ok so anywho, this lesson takes integrals as we have learned them a step further. Now, instead of finding the area beneath a curve on a given domain, we have to find the area between two different curves on a given domain. It's just a little extra wrinkle that we have to deal with, but no big deal. Let's say that we are given the following graph:



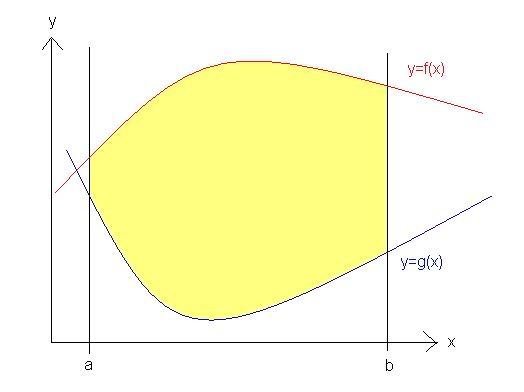
The red curve represents the upper curve, y=f(x), and the blue curve represents the lower curve, y=g(x). a and b represent the given domain, and the shaded yellow area represents what you are trying to find when you solve one of these problems. In order to find this area, you can use the following general formula:




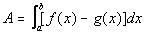
Now we can use that for a fun sample problem!! Brace yourselves...



First, we can draw the graph of this situation. The yellow graph is the area that we are trying to find.



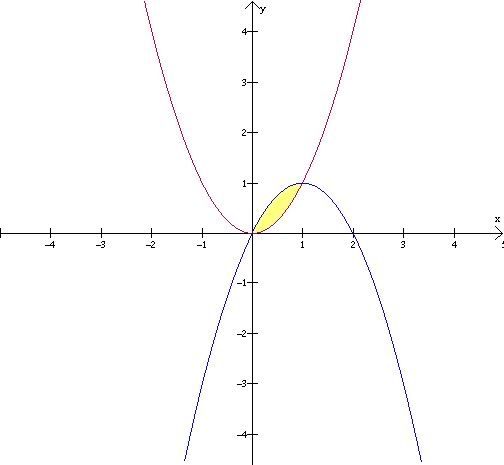
From this picture, we can see that the upper boundary is the blue curve, or y=2x-x(x), and the lower boundary is y=x(x). Therefore, the area is gonna be (upper boundary-lower boundary)dx or (2x-x(x)-x(x)). Also, the region is between x=0 and x=1. Therefore, the total area is



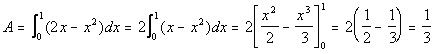
So, your answer is 1/3. YAY JESSICA YOU'RE NEXT HAVE FUN!!

Friday's Test Topics

Here’s a list of topics that will be covered on this Friday’s Chapter 5 Test.

Chapter 5 Test Topics
Fundamental Theorem of Calculus Part I (Sec. 5.3, #9,13,17)
Fundamental Theorem of Calculus Part II (Sec. 5.3, #13,41)
Substitution (Sec. 5.5, #13,23,278,31,37,41,57)
Evaluate an integral in terms of area (Sec. 5.2, #37)
Riemann sum: sketch, evaluate, explain and interpret (Sec. 5.1, #3,1,13,15)
Definite Integrals (Sec. 5.2, #33)
Net Change Theorem (Sec. 5.4, #47,48)

For additional practice problems, look at the chapter review (pp. 431-433)

That’s it! I’ll be around after school on Thursday and in early on Friday. Donut holes and OJ!

"It is inevitable that some defeat will enter even the most victorious life. The human spirit is never finished when it is defeated...it is finished when it surrenders."
Ben Stein

Here’s someone who refused to surrender to incompetence – I admire his patience, but I probably wouldn’t be able to last this long. It’s a fairly long audio clip (about 25 minutes) and I just want to say how thankful I am that MY students understand the importance of units...
http://media.grc.com/mp3/VerizonCantCount.mp3

And on a lighter note:

Section 5.5

This section is about the Substitution rule which allows anti-differentiation of complex expressions. The idea is to replace the complex section with a variable, (u), anti-differentiate, and then substitute back in the complex statement: a sort of inverse chain rule.

Substitution Rule for indefinite integrals

If u=g(x) is a differentiable function whose range is an interval I and f is continuous on I then
∫ f(g(x))g'(x) dx = ∫ f(u) du

This rule can also be applied to definite integrals by adjusting the range for u

∫ from a to be of [f(g(x))g'(x) dx] = ∫ from g(a) to g(b) of [f(u) du

Example

∫ (cos√t)/ √t

Given that u = √t then dt = 2du/t^-.5

substituting both expressions in removes the denominator and the roots to give "∫ 2cos(u) du"

antidifferentiate to get 2sin(u) + C and substitute the original expression for x to get 2sin√t + C




This is a helpful site: http://www.sosmath.com/calculus/integration/substitution/substitution.html

Alex you're next.