Today's lesson focused on "Limit Laws" and their uses:
There are eleven
limit laws:
1.) lim
x--> a[f(x)+g(x)] = lim x-->af(x) + limx-->ag(x)*Verbally, this means that the limit of a sum is equal to the sum of the limits
2.) lim
x-->a[f(x)-g(x)] = limx-->af(x) - limx-->ag(x)*Verbally, this means that the limit of a difference is equal to the diffenences of the limits
3.) lim
x-->a[cf(x)] = c limx-->af(x), where c is a constant*Verbally, this means that the limit of a constant times a function is equal to the constant times the limit of that particular function.
4.) lim
x-->a[f(x)g(x)] = (limx-->af(x)) (lim
x-->ag(x))*Verbally, this means that the limit of a product is equal to the products of the limits
5.) lim
x-->af(x)/g(x) = (limx-->af(x))/(limx-->ag(x)) -if limx-->ag(x) is not equal to zero.*Verbally, this means that limit of a quotient is the quotient of the limits(when and if the limit of the denominator is not zero)
6.) lim
x-->a[f(x)]^n = [limx-->af(x)]^n where n is a positive integer*Verbally, this means that the limit of a function raised to the power n is equal to the entire limit raised to the nth degree
7.) lim
x-->ac = c*Verbally, this means that the limit of a constant is equal to the constant
8.) lim
x-->ax = a*Verbally, this means that the limit of x as x approaches a is equal to a,
9.) lim
x-->ax^n = a^n*Verbally, this means that the limit of x to the nth degree as x approaches a is equal to a raised to the nth degree.
10.) This law is difficult to type of the computer, so I am going to verbally explain it. Basically this law states that the limit of the nth root of x as x approaches a is equal to the nth root of a.
11.) I will also explain this law verbally. It states that the nth root of f(x) as x approaches a is equal to the nth root of the entire limit of f(x) as x approaches a where n is a positive integer since you cannot take the root of a negative number.
Example Problems: What is another way to express the following limits using the laws listed above?
a.) lim
x-->2[f(x) + 5g(x)]b.) lim
x-->1[f(x)g(x)]c.) lim
x-->75*Answers and Solutions:
a.) Using law #1 above, we can see that the limit of a sum is equal to the sum of the limits. Therefore, lim
x-->2[f(x) + 5g(x)] is equal to limx-->2f(x) + limx-->2 [5g(x)]. Then, according to law #3, we can see that that the limx-->2[5g(x)] is equal to 5 limx-->2g(x). Therefore, the answer is limx-->2f(x) + 5 limx-->2g(x).b.) By using law #4, we can see that lim
x-->1[f(x)g(x)] is equal to the products of the limits of both f(x) and g(x) as x approaches zero. So, the answer is (limx-->1f(x))(limx-->1g(x)).c.) According to law #7, the limit of a constant as x approaches a is the constant. Therefore, the solution is the constant
5.Direct Substitution Property:lim
x-->af(x) = f(a)-functions with this property are continuous at a.
The Squeeze/Sandwich/Pinching Theorem:-If f(x)
<g(x)
<h(x) when x is near a (except possibly when x is at a) and the lim
x-->af(x) = limx-->ah(x) = L, then limx-->ag(x) = L.*If there is a function whose limit is difficult to find, and you know of two functions that surround the original function around the limit, then you can find the limits of the two surrounding functions, and if they are equal, you can assume that the limit of the original function is the same as well.
Example Problem:Find the limit of (x^2) sin(1/x) as x approaches 0.
Solution and Answer:Since the graph of
limx-->0 (x^2)sin(1/x) does not clearly show a limit, it is necessary to find two graphs whose limits would equal that of the original problem. So, we know that -1<sin1/x<1, and by multiplying each side by x^2, we get (-x^)2<x^2sin(1/x)<(x^2). From this we can find the limits of the graphs of (-x^2) and (x^2) as x approaches zero. We find that the limits of these two graphs as x approaches zero is equal to zero, then limx-->0(x^2)sin(1/x) is also equal to zero.Other Important Theorems:1.) lim
x-->af(x) = L if and only if limx-->a-f(x) = L = limx-->a+f(x)*Verbally, this means that the limit of f(x) as x approaches a is the limit if an only if the limits of f(x) as x approaches a from both the negative and positive sides is equal to the limit.
2.) If f(x)
<g(x) when x is near a(except possibly at a) and the limits of f and g both exist as x approaches a, then lim
x-->af(x)<limx-->ag(x).
Websites to help you understand the concepts of 2.3 more!
http://www.calculus.net/ci2/search/?request=category&code=1243&off=0&tag=9200438920658
http://www.geocities.com/mathdepot/squeeze.htm
Reminder to Jessica to write tomorrow's blog!
A couple jokes to keep you guys on your feet!
Q: What's the integral of (1/cabin)d(cabin)?
A: A natural log cabin!
Q: How does a mathematician induce good behavior in her children?A: "I've told you n times, I've told you n+1 times..."


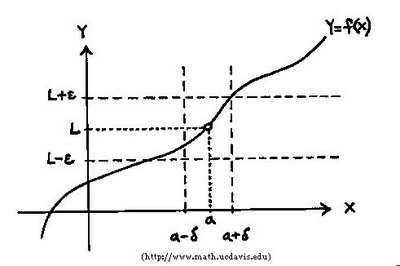


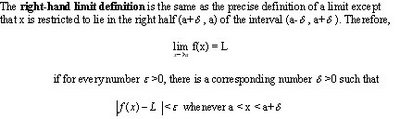
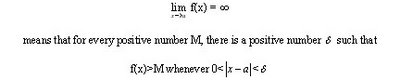
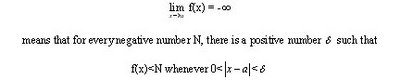

 *For limits, one-sided limits, and infinite limits, we can use the precise definitions to prove the limits convincingly instead of vaguely as we do with intuitive definitions.
*For limits, one-sided limits, and infinite limits, we can use the precise definitions to prove the limits convincingly instead of vaguely as we do with intuitive definitions.