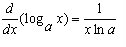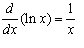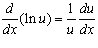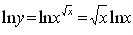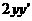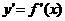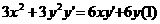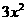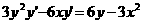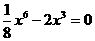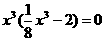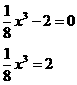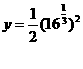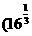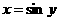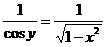3.7 Higher Derivatives

In today’s lesson, we learned that not only can you take a derivative of a function, you can take the derivative of another derivative as well!!! Let’s take a look:

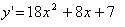(As usual, we are finding the derivative of the first equation)
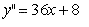(However, we can also find the derivative of the first derivative which is called double primes)
(We can even find the derivative again of double prime and make it triple prime)
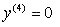(And lastly you can find the fourth prime which in this case is the final derivative possible since you have reached 0!)


Let’s look at some new notation we learned today that might be on the quiz/test/AAAPPP!!!!!

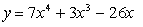
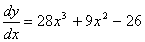(Now this derivative is finding the slope of the tangent line/ instantaneous rate of change)
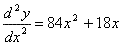(This shows how the derivative is changing)
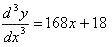(This shows how the previous derivative is changing as well)


You can also use the concept of Higher Derivatives on the Trigonometric Functions





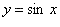
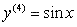
As you can see, the 4th prime equation is back to (sinx). This means that every fourth derivative in this situation repeats. Therefore could you find ?

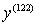If you divide 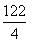, you will get 30 remainder 2. Thus you look at your double prime which is the second equation and you see that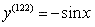


Now let’s use this concept on an exponential function:




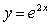
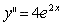
How about ?


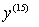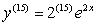
Finally why don’t you try a velocity/ acceleration problem which incorporates the higher derivative concept. If the function is given for the position of a particle, find:
1) Acceleration at time t. What is the acceleration after 4 sec?
2) When is the particle speeding up and slowing down? Show this through a graph for
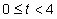
Velocity function(derivative of the position function):
Acceleration function (derivative of the velocity function) :
For the acceleration after 4 s, just plug it into the previous equation.



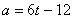
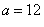
To find when the particle is speeding up and down, you must first equal the velocity function to 0.



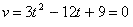
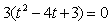
So at t=1 and 3, the particle is at rest.
Plug numbers in for t (in the equation ) and you will see that if the particle was moving before t=1, the particle has positive velocity, if the particle was moving between t=1 and 3, the particle has negative velocity, and if the particle was moving after t=3, the particle would have positive velocity.

How about acceleration? Make the acceleration function=0:
a=6t-12
0=6t-12
t=2; meaning at 2 seconds, the particle will have 0 acceleration.
Before t=2, the acceleration will be negative and after t=2, the acceleration will be positive.

Therefore, when the signs of velocity and acceleration are the same, the particle is speeding up. If the signs are opposite then it means that the particle is slowing down.


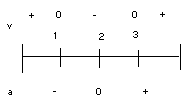
Speeding up:
Slowing down:

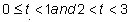
For more perspective:
http://tutorial.math.lamar.edu/AllBrowsers/2413/HigherOrderDerivatives.asp

Brian - you're next!

3.8 Derivatives of Logarithmic Functions

Hey class. Hope all of you enjoyed homecoming. Sorry that the game wasn't much of a show. Poly next week though so keep up the spirits. Well its time for math again, and this concept can be pretty difficult.

There are two basic equations in this section that the others are derived from:
For the first equation it is 1 over both x and ln of the base a

and the second equation is simply one over x when taking the derivative of the natural log of a number

From the second equation, if the the "x" is a polynomial or complex equation that we'll designate as "u" then it is 1 over the equation "u" multiplied by the derivative of that equation:

Logarithmic Differention is basically just applying logarithmic rules to simplify an equation so that its derivative can be taken easier.

Here is a simple example from the book of logarithmic differentiation:

Differentiate:

1. In the first step we took the natural log "ln" of both sides, and therefore the exponent came down.
2. In the next step using the product rule we took the derivative of that term. Specifically we took the first term times the derivative of lnx which is 1/x plus lnx times one over twice the square root of x.
   
3. In the third step we multiplied y to both sides in order to isolate y' on one side.

To express e as a limit:
As x approaches zero

As n approaches infinity


Additional Links
Another Review
A GREAT place to practice derivatives of logs with sample problems and solutions


MAGNUS you're up next.




This is Maurice Drew, he came out of UCLA last year so this is his rookie season. He's 5'7" and thats football height so he's probably shorter and 200 pounds. His legs as you can see are ginormous and people often mistake him for having pads on when he does not. This season he has 187 yds. and 3 touchdowns.


This is Mr. C who taught geometry here last year as well as coached the 400 team. He is really fast. He holds the prep league record in the 400 and the 200. Mr. C ran track in college at Amherst. He is currently in med school at USC.

3.6 Implicit Differentiation

Hey guys, this is Ismael if you hadn’t already guessed. Today we learned about implicit differentiation. Implicit differentiation is different from explicit differentiation in that the explicit functions we have dealt with so far only deal with expressing one variable explicitly in terms of another variable. Implicit functions express the relationship between y and x implicitly. For example:

Explicit


Implicit


The implicit equations can be used to draw the graph of a circle. By solving
for y you get .The function is the upper half of the circle and the function is the lower half of the circle. Graphing this function gives us:


The tangent lines represent the derivatives of both functions when x=5.

You can differentiate implicit functions like these by this method:


Use the Chain Rule:
This is the same thing as saying because y=f(x) and . Therefore:


Here is an example of this method of using implicit differentiation to find y' (the slope):

Note: because we are not dealing with x in this case; we are dealing with y, which represents a function. Therefore, it is necessary to take the extra step of taking the derivative of the inside function, which is y. As a result .

Let's continue:


Now move over the and the 6xy' terms to the opposite sides of the equation so that they switch places.

This allows us to factor out y prime


Now we know the slope of the function. Let’s say we had to find the slope of the implicit function at the point (3, 3). We would simply plug in x=3 and y=3 into the equation we derived for y'.

Use the point slope formula:

Let’s say we were to find the points on the graph at which the slope of the tangent line was 0. First, you would set the equation for y' equal to 0.

Now we plug what we got for y into the original equation.


Bring to the other side of the equation:


Now we think: for what values of x would the left side of the equation equal zero? One value, obviously, it would be x=0. To find the second one, we first divide both sides by , giving us:

We then multiply both sides of the equation by eight and get:

Therefore, the values at which the derivative of the graph is zero are and x=0. To find the y values, simply plug in the x values into the equation .

Therefore, the points on the graph at which the tangent line is horizontal to the curve are: (0,0) and ,.

Now, we move on to inverse trig functions!
Let’s say we have
That equation is the equivalent of
By implicit differentiation:



By using our Pythagorean rule for the relationship between sine and cosine
( ) we can come up with:



(Note: We can replace with because of our original equation: )


Therefore,

You can look at page 233 in our text book for the table of all of the derivatives of the inverse trigonometric functions.

By the way, Ami, you are next for the blog posting.

Here are a couple of links supporting the Topic of the Day:
http://archives.math.utk.edu/visual.calculus/3/implicit.7/index.html

http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/implicitdiffdirectory/ImplicitDiff.html

And to end this blog with a bang, here are a few Ben Franklin quotes:

"Anger is never without reason, but seldom a good one"

"Do not fear mistakes. You will know failure. Continue to reach out."

"Either write something worth reading or do something worth writing."

"Employ thy time well, if thou meanest to gain leisure."

"Experience is a dear teacher, but fools will learn at no other."

And some silly quotes:

"Sure there have been injuries and deaths in boxing - but none of them serious." - Alan Minter, Boxer

"I think that the film Clueless was very deep. I think it was deep in the way that it was very light. I think lightness has to come from a very deep place if it's true lightness." - Alicia Silverstone, Actress

"How to store your baby walker: First, remove baby." - Anonymous Manufacturer

"You guys line up alphabetically by height." - Bill Peterson, Florida State football coach

"Men, I want you just thinking of one word all season. One word and one word only: Super Bowl." - Bill Peterson, football coach

"The internet is a great way to get on the net." - Bob Dole, Republican presidential candidate